Diffusion

Likely publishing this at some point, not releasing the technical details just yet! If you want to discuss the math and code with me, please contact me! Collaborating with Marc Schlicting and Mykel Kochenderfer (SISL).

Pretty realistic images of streets generated by a computer after training a diffusion model. Leftmost column shows starting noise and rightmost column presents artificial images.

Overview

Collecting autonomous driving data is expensive. It takes a long time to deploy a vehicle across diverse environments, process the data, and apply it to downstream perception tasks - such as object detection, classification, segmentation, and tracking - for a self-driving vehicle (SDV). Furthermore, this data collection is financially-intensive. While there are many autonomous driving datasets, they are limited in geographical diversity (many with a focus on San Francisco). In short, it is impractical to collect numerous geographically-diverse datasets and thus difficult to promote sufficient diversity in training an SDV, which is important to generate robust self-driving cars.

Recently, there has been significant research in using generative technolo- gies to create image data. This includes variational auto-encoders (VAEs), generative adversarial networks (GANs), and diffusion model (DMs) - each with their own flavours. Diffusion models are known to be the most stable of existing options. Therefore, our problem statement is:

Objective

Generate artificial AV images to improve robustness in a downstream perception task. More specifically, explore us- ing diffusion models to generate the images and test whether a diffusion-augmented dataset improves object detection.

Data Centric Approach

The first step is creating a baseline, which generates new images without using generative models (e.g., DMs). Initially, my work entailed running many simulations that generate artificial datapoints (instead of datasets) in a simplified use-case using a toy dataset and a strategy that doesn’t have anything to do with the parameters of diffusion models. I call this a “data-centric” approach, which constructs a lower-dimensional embedding of an original dataset (eg. using PCA), finds empty “pockets” in the embedding space, and inverse transforms these pockets into the higher dimensionality of our original dataset. Formally, we fix a tabular non-image dataset, namely \(D\) (which ideally represents a driving image dataset). Then we construct a lower-dimensional embedding of \(D\) (e.g., using PCA), \(D' = \text{PCA}(D)\) with the intent of finding empty “pockets” \(P\) in \(D'\). Once they’re identified, we inverse transform them back to the original dimensionality of \(D\), that is: \(P = \text{invert}(P)\). Then, we construct an augmented dataset \(A = D \cup \text{label}(P)\) using a semi-supervised algorithm \(\text{label}\), and compare performance.

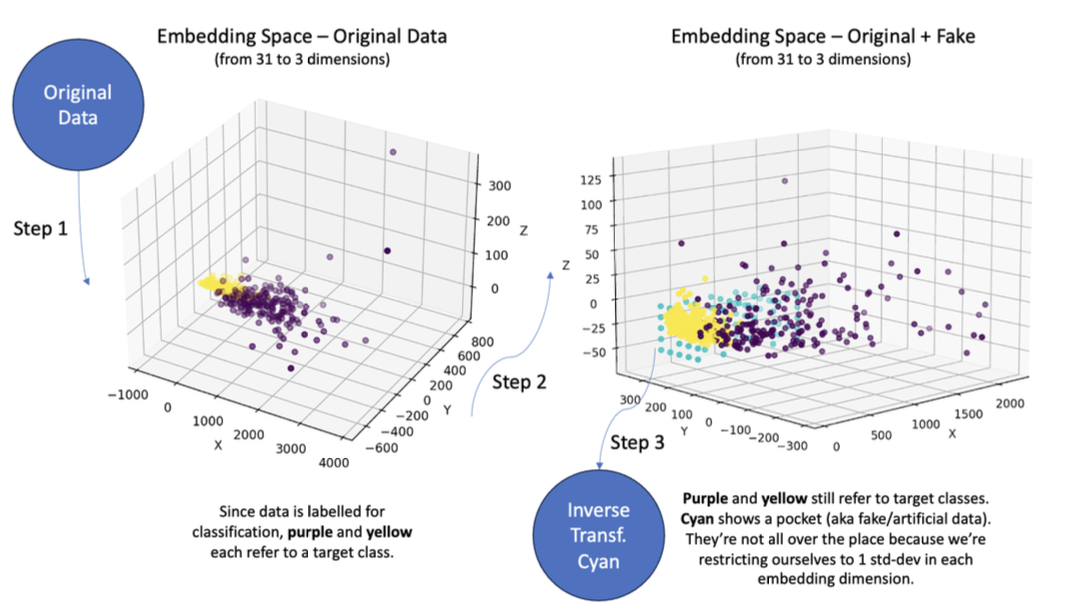
Figure 1: Visualization of data-centric approach. Yellow and purple are target class labels for \( D \) and cyan represents candidate pockets \( P \) in the embedding space. Very rarely does artificial data help with the downstream task of classification, but in a few special cases it does, improving test-accuracy by 4 to 5% on a test set. This exploration demonstrates that the data-centric approach holds promise, to an extent.

These pockets are subsequently ranked for usefulness and sequentially augmented with the original data, after which performance w/ and w/o augmentation on a downstream task (eg. classification) is observed. I’ve noticed that very rarely does artificial data – at least the way I’m generating it – help with a downstream task (in this case classification), but in a few special cases, it nevertheless does! A visual is shown below:

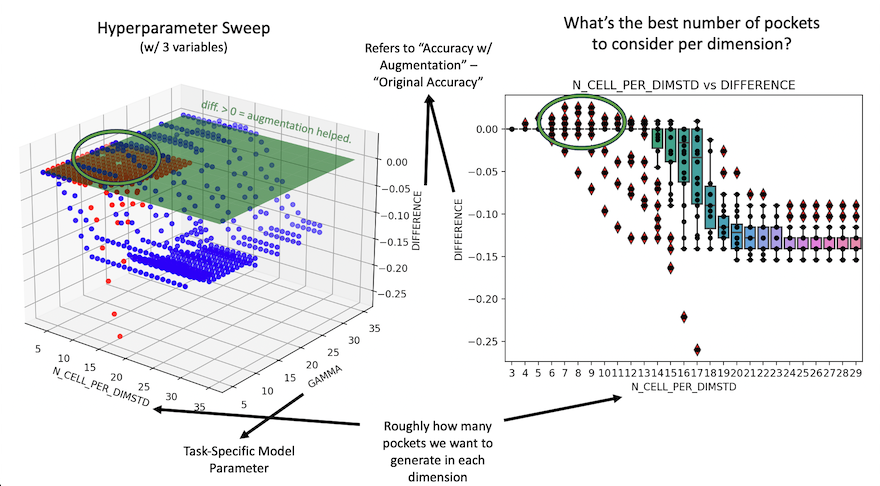
Figure 2: Image of the quality of classifcation with and without augment with and without pockets.

This exploration shows that some parts of my data-centric approach of generating artificial data (much of which is applicable towards the other “model-centric” of generating artificial data) hold promise. The next steps are to train some diffusion models on driving data and test out this “pocket-finding” approach on an embedding of diffusion model parameters!

Model-Centric Approach

Given \(n > 1\) AV image datasets, and \(i \in [0, n]\), the next step is to train a \(\text{DM}_i\) for each driving dataset \(\mathcal{D}_i\) and test out the “pocket-finding” approach given a set of datasets \(\mathcal{D}_{\text{META}} = \{\texttt{embed}(\text{DM}_i)\mid\forall i \leq n\}\)! Note that we use latent diffusion models instead of original DDPMs for computational efficiency which diffuse on VAE-latent representations.

Figure 3: Example images reconstructed very well by a VAE.

Results and Next Steps

Actually applying the pocket-finding approach on diffusion models is quite complex and immediately unrealistic – diffusion models, even latent diffusion models, have an enormous number of parameters. Pocket-finding in such a high-parameter space, or even a lossy embedding of this space (not to mention the non-negligible loss of information were one to do this), is intractable. Ultimately, my collaborator and I have architected some methods to make out final goal – to generate new, out-of-distribution autonomous driving datasets – much more tangible. I’m intentionally leaving out some of the details here given the work is in-progress, but here’s an image of a diffusion model trained on the Waymo dataset (the same one from the top).

Figure 4: Reverse process of a latent diffusion model trained on street views and traffic scenarios. Leftmost column shows starting noise and rightmost column presents artificial images. Trained for approximately 48 hours on subset of Waymo and Nuimages Perception Datasets on 2-4 V100 GPUs